怕自己理解得不够透彻, 先附上优酷视频.
旋转术语
对于左手坐标系非常好理解, 想象自己用第一人称视角开飞机, 左手坐标系Z轴(纵深)指向屏幕里, 也就是飞机面朝的方向.
1. 沿X轴 - Pitch - Lateral - 俯仰. 飞机抬头升起, 或低头俯冲.
2. 沿Y轴 - Yaw - Vertical - 偏航. 飞机在水平方向上调整航线(朝向).
3. 沿Z轴 - Roll - Longitudinal - 桶滚. 飞机朝向(前进方向)不变, 但像一个钻机一样旋转/摇晃.现在在万向节中想象你在开飞机, 它的朝向由箭头标识, 这样很快就能确定陀螺仪的旋转轴, 是么? 图中已经用各自颜色标注.
当然, 你知道了Pitch/Yaw/Roll也不一定有机会开飞机, 也许这些东西还可以用在更普遍的地方. 比如游泳/跳水/打篮球/滑板/滑雪, 你能通过它们来表达自己或者别人(电视上?)完成的旋转是怎么组合起来的.
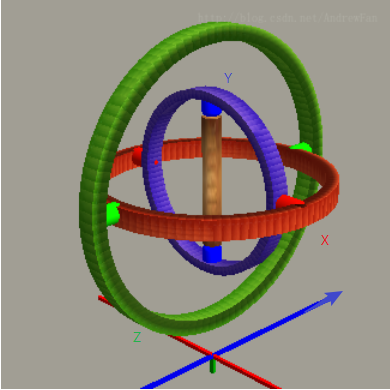R-Pitch, G-Roll, B-Yaw
开飞机
对于万向节(平衡环架), 其实是保持中心的转子平衡的一种装置.
把它用在开飞机上, 这个飞机可能开起来还不太一样, 会有点像是开高达. 也就是不管外面的高达是横是竖, 里面的驾驶员始终保持站立姿势.
假设, 有一种气流我们称之为螺旋气流, 会分别从三个方向袭来, 试图改变飞机的轨迹, 驾驶员该怎么做呢?
迎面袭来螺旋气流, 可以通过Roll进行调节, 像这样:
G-Roll
从侧翼袭来螺旋气流, 可以通过Pitch进行调节, 像这样:
R-Pitch
从顶部袭来螺旋气流, 可以通过Yaw进行调节, 像这样:
B-Yaw
陀螺仪来保持飞机稳定性, 看上去没什么问题. 但是, 会有这种情况, 当驾驶员垂直向上飞行时, 也就是这样
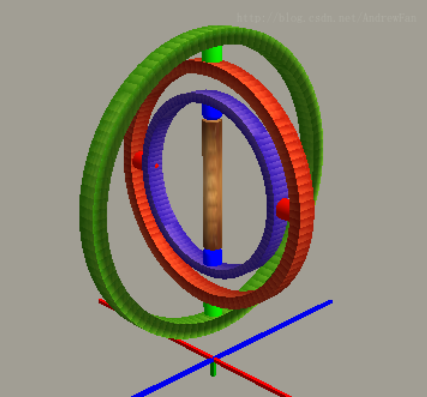驾驶员在尝试将一枚核弹送向外太空的敌舰
此时从Z轴方向(也就是飞机的顶部)袭来螺旋气流, 飞机是毫无招架能力的. 你会发现, 无论怎么旋转, 中间的立柱(转子)无法保持稳定.
*这就是钢铁侠不愿意回忆进入虫洞的原因吧, *为这种飞行方式简直就是跟死神赌博]
特点:
上面的旋转轴嵌套关系为 ZXY, 所以旋转时会有这种关系.
1. Roll - 任何轴向都不改变, 局部坐标系不变. 因为没有变化, 3个轴保持正交关系.
2. Pitch - 改变Z轴朝向, 局部坐标系改变.
3. Yaw - 同时改变ZX轴朝向, 局部坐标系改变. 尽管改变了两个轴的朝向, 3个轴还是保持正交关系.这就有个问题, 比如仰起了90度的情况, 其实Pitch操作已经改变了局部坐标系的Z轴.
此时我们在世界坐标系下做Roll, 对于局部坐标系其实是Yaw的操作.
但是为了保持转子平衡, 局部坐标系的Y轴保持不变, 结果就和改变后的Z轴重合了. 所以世界坐标系Z轴旋转, 干的其实是Y轴的活, 而且在同时改变3个轴的朝向(注意和最开始的Roll不一样)
所以我的问题是, 为什么一定要保持转子平衡呢? 如果在Pitch的时候也同时改变Y轴方向, 始终保持3个轴在局部坐标系中正交, 不就不会有这种死锁问题了么.
转子平衡 vs 避免死锁 不可兼得.
除非, 在此基础上再加一个最内层旋转轴, 这样我们就一共有4个旋转轴了…这是否就是四元数的图形含义呢?
当然转子平衡是一说, 旋转又是一说.
我们在引擎中做物体旋转的时候, 更在意的是’这个物体是否能够旋转到我们所期望的那个朝向’, 而不是去想象里面有个驾驶员在前仰后翻.
Unity中的万向锁
Unity欧拉角的旋转顺序（父子关系）是y-x-z。即旋转y轴x和z轴都变，旋转x轴只有z轴变化，旋转z轴其它轴不变.
在Unity中创建两个嵌套的Cube, 坐标系在局部(local)和惯性(global)之间切换, 修改根Cube的Rotation来观察Unity3D旋转的规则
- GameObject上Transform组件上的Position Rotation Scale 都是相对于父对象的局部信息. 对父对象的Transform做出修改, 会嵌套的作用在子对象上, 但子对象的Transform因为都是局部数据, 所以会保持不变.
- (按某个轴)旋转, 既不是依照惯性坐标系, 也不是依照局部坐标系. 而是依照欧拉角的旋转顺序做出改变. 比如
- 旋转X轴一定角度之后, 旋转Y轴. 你会发现此时的Y轴与惯性坐标系一致. 那是因为y-x-z嵌套关系中, 旋转X轴不改变Y轴.
- 旋转X轴一定角度之后, 旋转Z轴. 你会发现此时的Z轴与局部坐标系一致. 那是因为y-x-z嵌套关系中, 旋转X轴改变了Z轴.
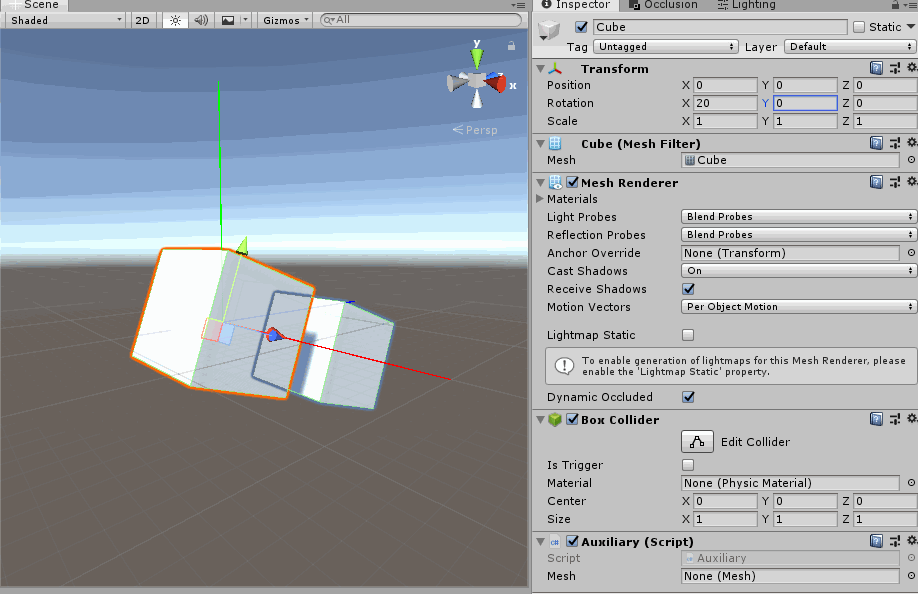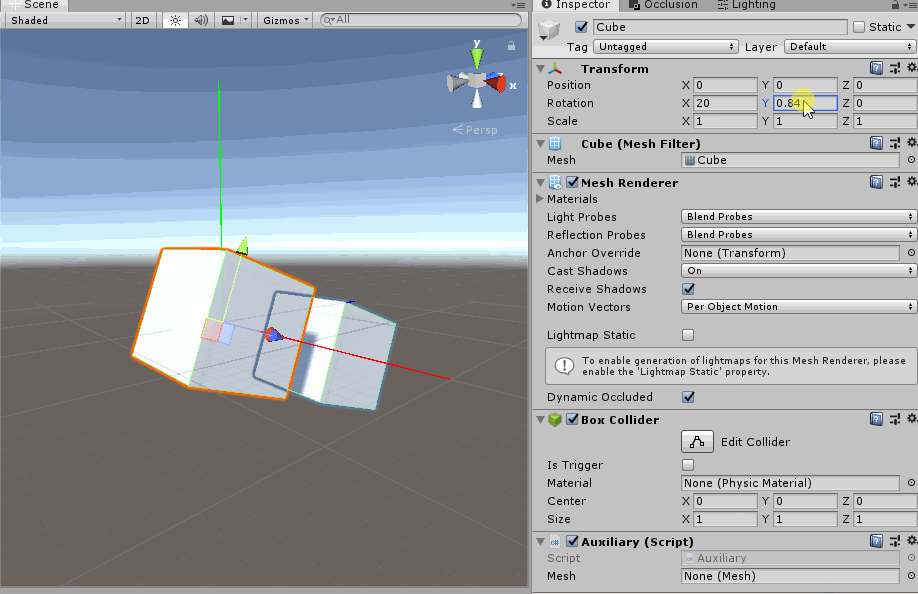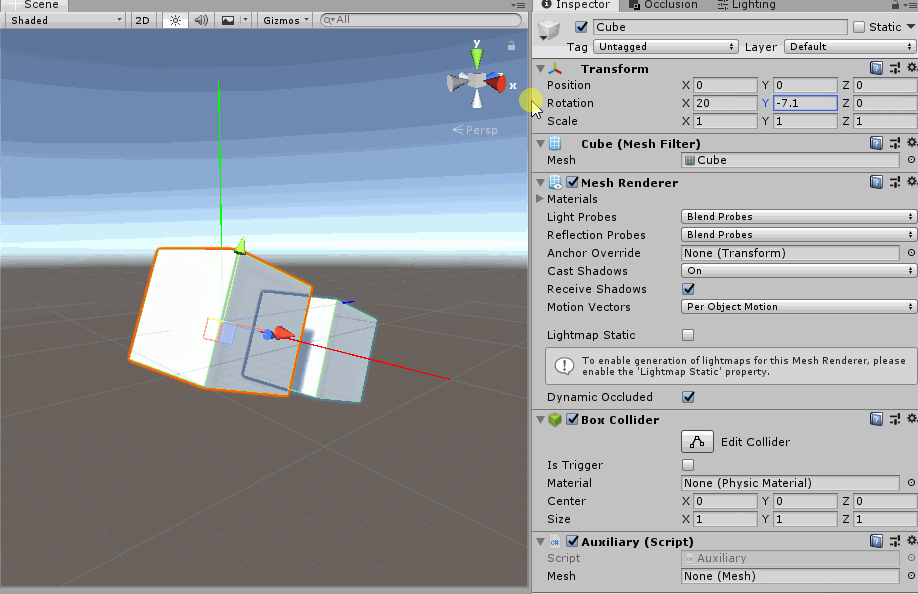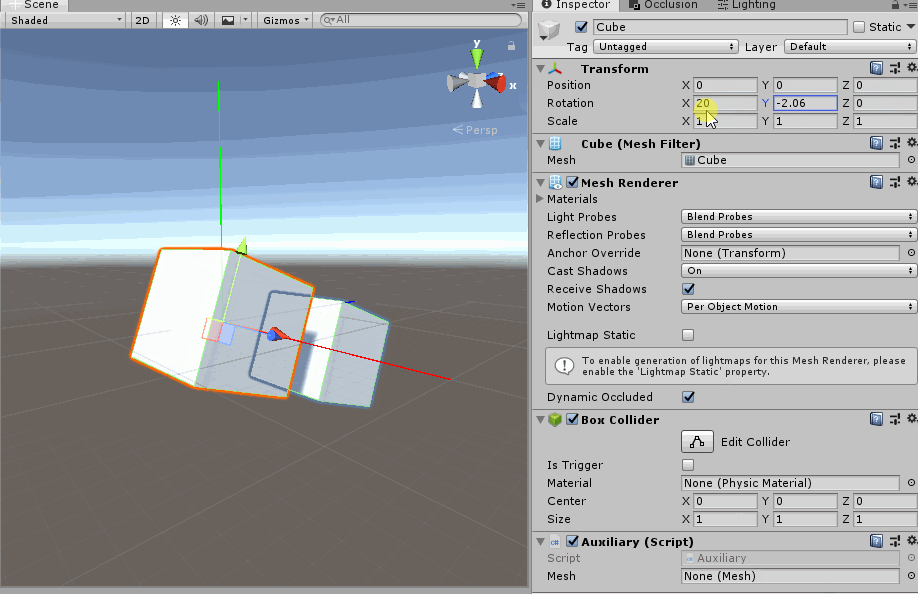旋转X轴一定角度之后, 旋转Y轴
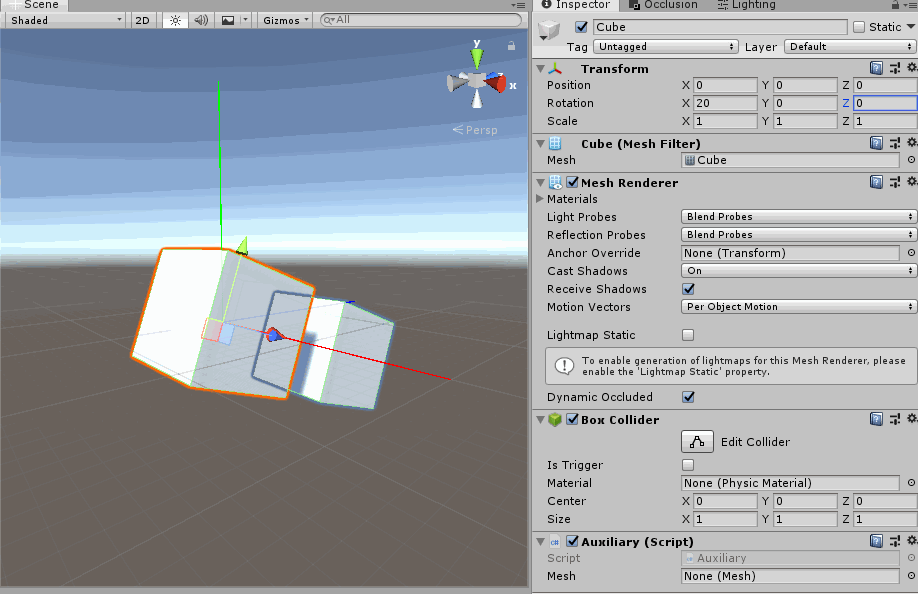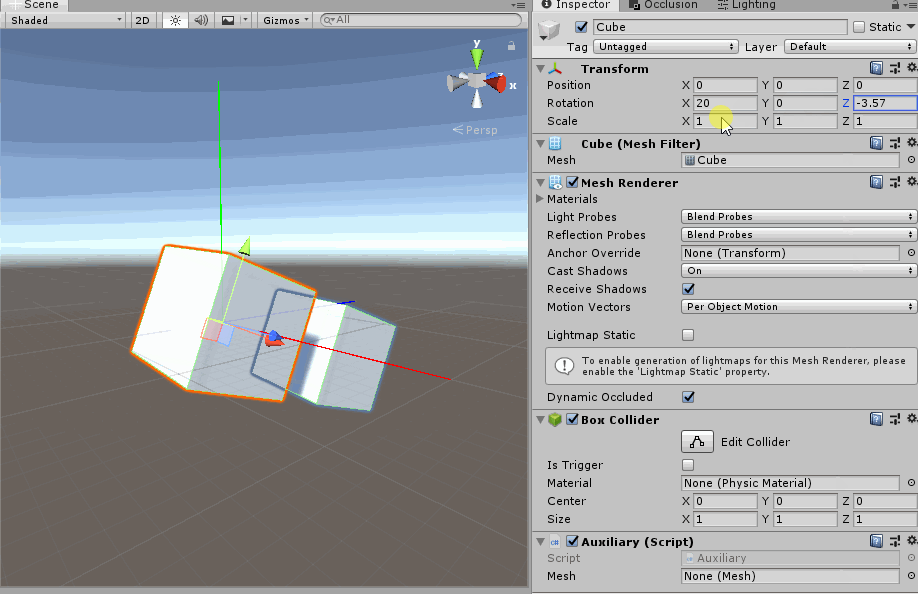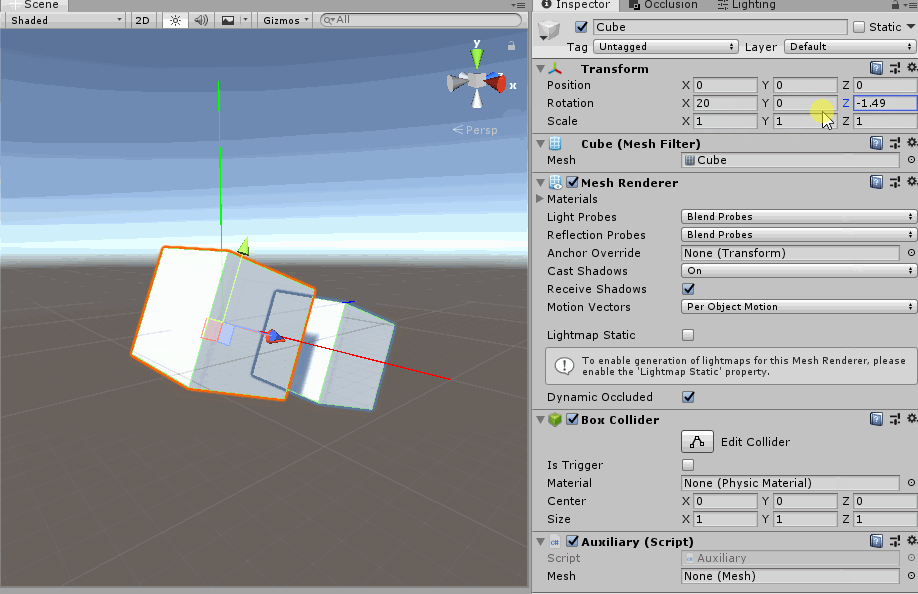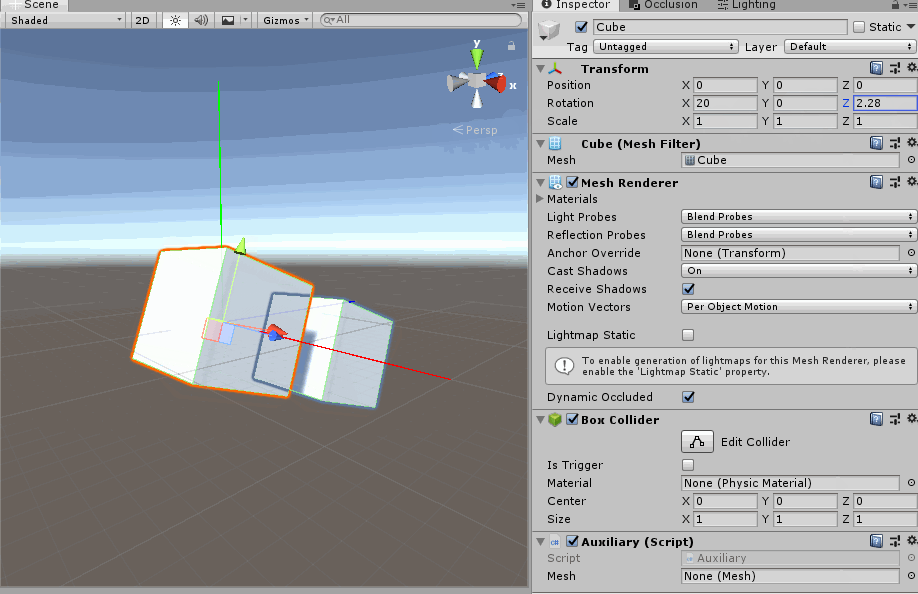旋转X轴一定角度之后, 旋转Z轴
这就导致, 如果有多个方向的旋转, 严格按照y-x-z的变换顺序, 才能保证所有的旋转作用在局部坐标系下.
旋转规律和我们的示意图是一致的
如果反过来, z-x-y的顺序做旋转, 传入的角度应该是按照惯性坐标系来计算的.
但这只是计算顺序, 无法解决万向锁.
当X轴旋转-90°, 让Z轴和Y轴重合, Z轴向的旋转也就是Y轴的旋转, 即这两个Rotation向量结果是一样的
- -90, 45, 45
- -90, 90, 0
这个症状可以描述为: Pitch90°的同时, 无法完成Yaw的动作.
在U3D中，旋转顺序是y-x-z（模型坐标—惯性坐标系旋转），官网为z-x-y（惯性坐标系—-模型坐标）。
y轴是惯性坐标系的y轴，其它轴是模型的坐标轴。这是因为不同坐标系的轴才有可能产生共面.
我一直想的是, 在这个飞船Pitch转体的同时, 加上Yaw转体是个什么样子, 这样的动作能飞过什么形状的洞口
然后就是那些极限运动类的模拟器(游戏), 一个滑板运动员冲上弧形斜坡, 准备在空中实现Pitch转体时, 再同时完成Yaw, 好像也挺常见的.
所以万向锁在Unity中就真的锁住了么?
Unity的解决方案
旋转的起点
所有的旋转都是从 (0, 0, 0) 开始. 而不是像我想象的那样, 旋转一定角度之后, 保持这个状态, 下次旋转从这个状态开始, 哪怕它锁住了.
其实这就保证了物体能正确地转到我们想要地任意角度了.
Rotation 中的数据是记录下来的, 这个值是局部坐标系的值, 用于每一帧渲染的时候, 对象变换的嵌套计算, 最终才会确定对象的状态.
Root对象的局部坐标系就是惯性坐标系(与世界坐标系平行), 一切都是从0开始, 而不是相对于上一个状态去做Δ角度旋转.
所以没有机会锁住.
表现手法而非实际实现
我自己也很纳闷的这种设计, 为什么一定要这样: 转Z轴谁都不改变, 转X轴改变Z, 转Y轴改变XZ.
就不能转任何轴都一起改变, 或者转任何轴都不改变其他轴么?
也就是完全的局部坐标系, 或者惯性坐标系.
或许这和坐标系统设计有关系(矩阵变换都是作用在物体的局部坐标系上的), 或者也可以理解成人为设计就是这样.
Unity提供旋转计算的API都是使用的四元数, Rotation 仅仅是给人看的(我们似乎不能直接通过代码改变它), 因为它比较直观.
关于四元数的资料请看
- <3D数学基础:图形与游戏开发> 10.4 四元数
- <游戏引擎架构> 4.4 四元数
- 【Unity编程】四元数(Quaternion)与欧拉角
- 四元数与三维旋转
- 四元数的可视化
- 四元数和三维转动，可互动的探索式视频
- Visualizing quaternions - An explorable video series
利用它的规律
上面产生的死锁, 是因为旋转X轴后, X-Z平面坐标系(局部坐标系)与Y轴坐标系(惯性坐标系)不一样了.
万向锁的根源就是 旋转轴不在同一个坐标系中
使用的角度应该遵循这个规律: 对Y轴使用惯性坐标系下的角度, X-Z轴使用局部坐标系下的角度.
最后附上飞机的简易结构图.
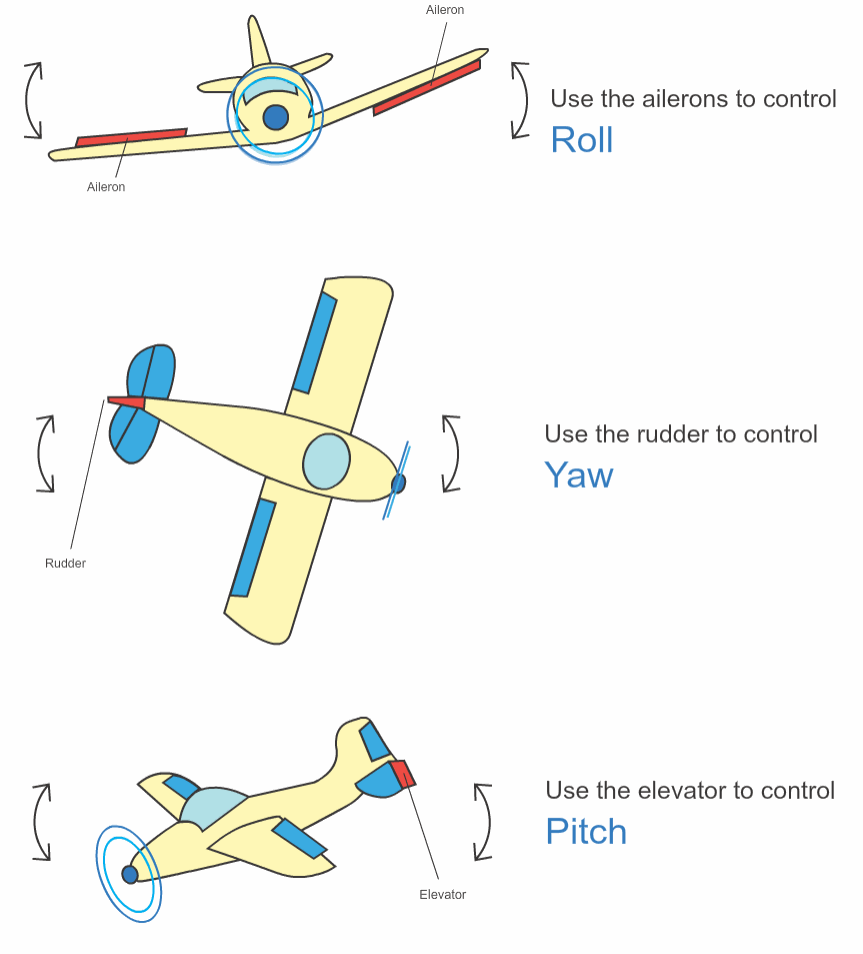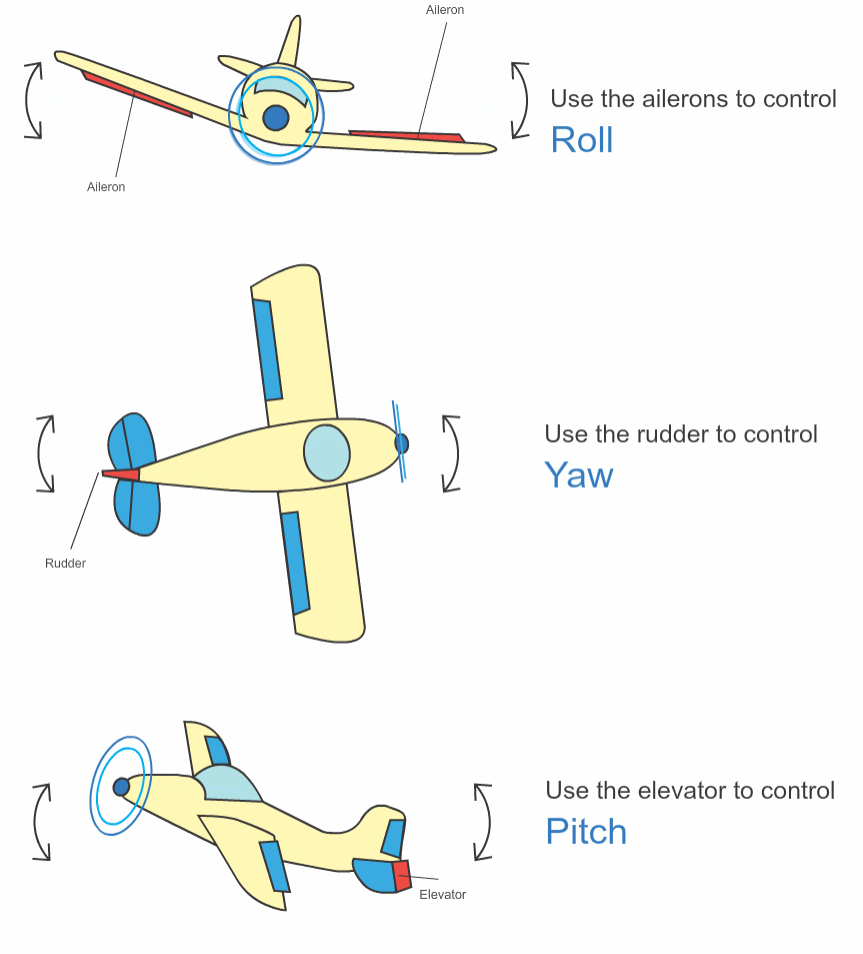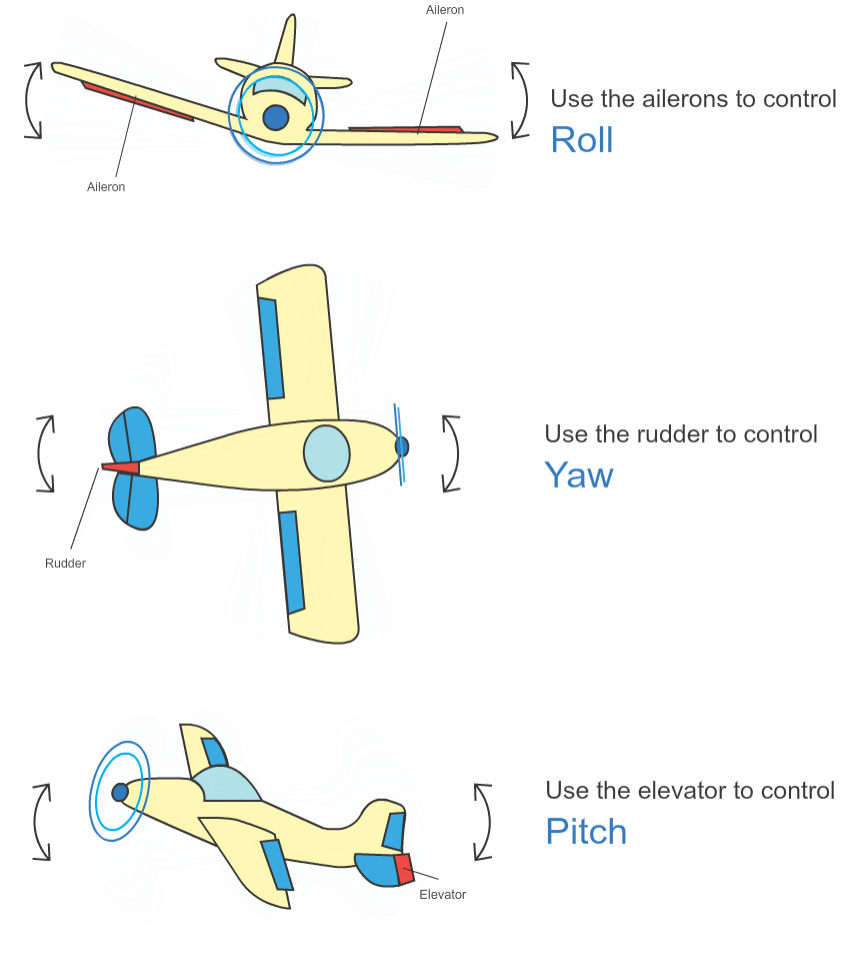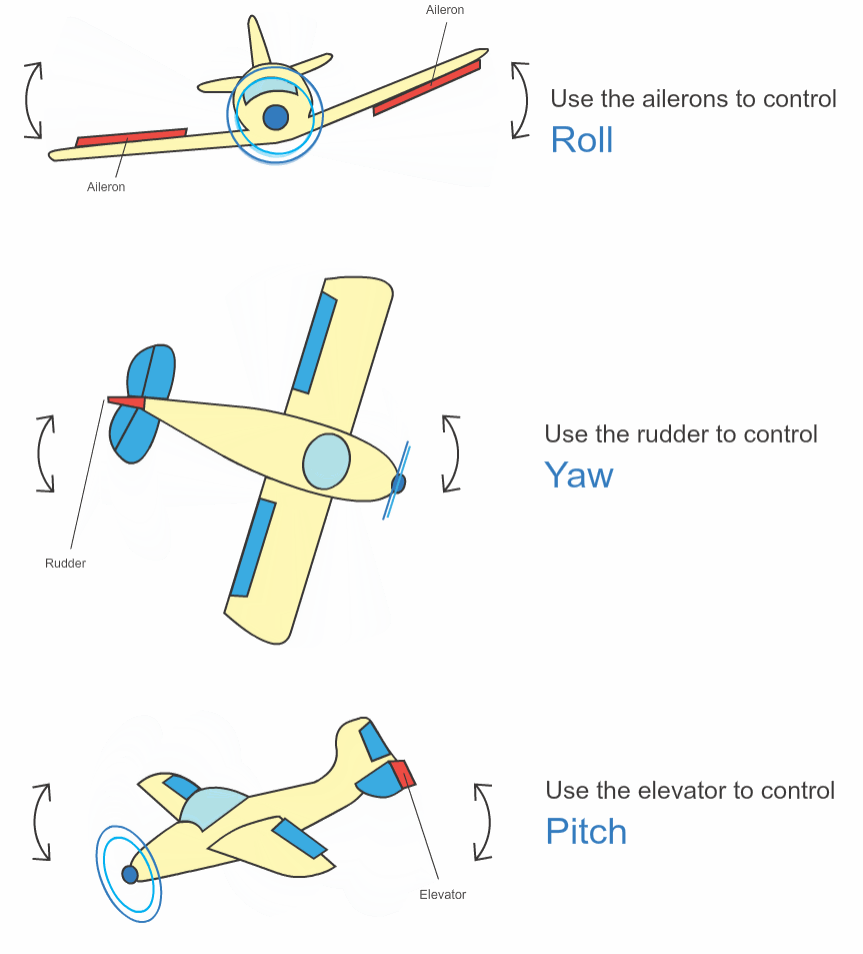Pitch-Elevator-升降舵, Roll-Aileron-副翼, Yaw-Rudder-方向舵
还有我为什么要研究万向锁…
这个辅助很有内涵